This article deals with:
Naar aanleiding van de controle op wisselend vloeien voor ondergrondse transportleidingen wil ik wijzen op het navolgende.
In het normatieve gedeelte van de NEN3650 wordt er bij de bepaling van wisselend vloeien alleen gesproken over hoofdspanningen, in Bijlage C11 (voorbeeldberekening) wordt in par.5.1 e.v. gesproken over spanning in langsrichting en omtreksrichting. In beide paragrafen worden deze spanningen uitgezet langs de horizontale en verticale as van de vloei-ellips.
In de voorbeeldberekening is men er van uitgegaan dat de schuifspanning 0 is. Alleen in dat geval komen de hoofdspanningen overeen met de spanning in langs- en omtreksrichting wat betreft grootte en richting.
| PLE berekent de hoofdspanningen met: | 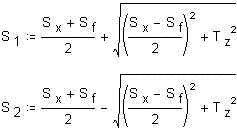 |
Hierdoor is S1 per definitie > S2.
In het normatieve gedeelte van NEN3650 staat op pagina 66 de vloei-ellips getekend. Hierbij is de S1 op de horizontale en S2 op de verticale as gepositioneerd. Nu levert dat problemen op wanneer de hoofdspanningen t.g.v. veranderende belastingen gaan roteren. Men dient dan de hoofdspanningen continu te volgen om te weten welke hoofdspanning de eenmaal gedefinieerde S1 resp. S2 is. Het is daarbij mogelijk dat de hoofdspanning (S1), welke in het begin de grootste was, na verloop van tijd even groot is geworden als S2 en vervolgens kleiner wordt dan S2.
Wanneer zo'n situatie zich voordoet, gaat PLE in de fout omdat PLE S1 als de grootste van S1 en S2 definieert.
Werkwijze op dit moment.
Door de afschuiving Tz te verwaarlozen valt Sx samen met S1 en Sy (of Sf) samen met S2. Uitgaande van de locatie op het knooppunt (0-90-180-270) met hoogste von Mises-spanning wordt vervolgens een vloei-ellips getekend met daarin de doorlopen trajecten (Leiding koud, Leiding koud+druk, Temperatuur + druk etc.).
Met behulp van liniaal, potlood e.d. wordt vervolgens bepaald of wisselend vloeien optreedt op de manier van het voorbeeld uit bijlage C11 van NEN3650. Men vergeet daarbij dat de situatie in dit voorbeeld relatief simpel is. De rondgaande spanning blijft daarin tijdens het opwarmen van de leiding namelijk constant. Wanneer dan bij een zekere temperatuur het lineair elastisch berekende traject de vloei-ellips (in punt IV) snijdt, blijft bij verder opvoeren van de langsbelasting het spanningspunt op IV liggen.
Wanneer nu het lineair elastisch berekende traject niet evenwijdig aan één van de hoofdspanningsassen loopt, (zoals bij bochten het geval is) en de vloei-ellips snijdt, is het moeilijk te voorspellen hoe het werkelijke spanningstraject gaat lopen. In zo'n situatie is de vloei-ellipsmethode nauwelijks bruikbaar.
Voorgestelde werkwijze.
Op blz.66 van NEN3650 wordt eveneens de schuifspanningshypothese voor wisselend vloeien genoemd. Op blz. 67 wordt een heel beperkte samenvatting van deze methode gegeven.
Deze methode wordt uitgebreider behandeld in Stoomwezen blad D1200 en ASME VIII div.2 appendix 5. Wij beperken ons nu tot ASME omdat dit document oorspronkelijk de basis is van D1200 en NEN3650.
In ASME par 5-110.3a staat:"When Principal Stress Direction Does Not Change."
In ASME par 5-110.3b staat:"When Principal Stress Direction Changes."
De trajectbeoordeling volgens ASME VIII div.2
De ASME maakt onderscheid tussen twee gevallen:
Uit alleen de spanningsresultaten op tijdstip t0 en t1 valt niet vast te stellen welke hoofdspanning S1 genoemd moet worden op tijdstip t1 . Grootte en richtingen van de hoofdspanningen geven daarover onvoldoende informatie, want S1 kan best over b.v. 90 gedraaid zijn en van de kleinste de grootste hoofdspanning geworden zijn. Men kan S1 op tijdstip t1 slechts dan benoemen, wanneer men S1 tussen t0 en t1 van moment tot moment heeft gevolgd.
Bij de aanpak volgens 5-110.3(b) hoeft men zich geen zorgen te maken over welke hoofdspanning we spreken. Deze paragraaf geeft nl. een algoritme om het maatgevend traject te bepalen m.b.v. de trajecten van de componentspanningen en deze spanningen zijn altijd duidelijk gedefinieerd. Wanneer de schuifspanningen niet verwaarloosbaar klein zijn, is deze methode dan ook de enige, die algemeen bruikbaar is.
Aangezien wij voor een algemene werkwijze niet zondermeer kunnen aannemen dat de richtingen van de hoofdspanningen niet veranderen, volgen wij hieronder de werkwijze van ASME VIII div.2 app.5 clausule 5-110.3b, wij handhaven echter de notatie van de spanningen zoals die staan in de NEN3650.
We kiezen een zwaar belast punt P van de constructie, waarvoor we het spanningstraject willen beoordelen.
Voor een twee-assige spanningstoestand halen wij Sx, Sf en Tz in P uit de PLE tabel T620-33. Dat doen we voor alle belastingsgevallen die in de loop van de tijd optreden.
Sx, Sf en Tz kunnen we dus als functies van de tijd zien: Sx(t), Sf(t) en Tz(t).
| Stap 1 |
|
| Stap 2 |
|
| Stap 3 |
|
| Stap 4 |
|
| Stap 5 |
|
| Stap 6 |
|
The following loading conditions should be considered:
Although NEN3650 requires these calculations to be made they are seldom provided. As can also be seen in our next example.
The loadings:
1 Pre-stressed line, cold
2 Cold line, pressurised with settlement
3 Hot line with pressure and settlement
4 Settlement only.Result in:
The yield-envelope at this location looks like this:
Op de methode met de vloei-ellips beschouwen wij het traject 1-3 als maatgevend.
Traject 1-3 heeft een maximum ratio van 1.008 bij 270 en is dus maatgevend met de ASME methode zoals blijkt:
De nu gebruikte uitgangspunten en programmatuur blijken niet overeen te komen met het gestelde in ASME. Beschouwen we de ASME methode nauwkeurig, dan constateren wij verschillen met D1200 en NEN3650. In D1200 moet men de range bepalen uit SABmax-SABmin, dit is m.i. niet correct.
SABmax wordt bepaald met een referentie-case die niet dezelfde hoeft te zijn als de referentiecase van SABmin. Als bovendien de beide S-spanningen van teken verschillen rolt er een grotere waarde uit.Lezen we ASME nauwkeurig dan staat dit er ook niet. Daar wordt de maximum waarde berekend van |SAB|. Voeren we de berekening op deze manier uit dan geeft het grootste traject (1-3) een ratio van 1.008. Kleinere trajecten geven een kleinere ratio, dit in tegenstelling met de manier van D1200 en NEN3650.
Kijken we naar de vloei-ellips dan is de ASME methode logisch, immers '1' is het verst verwijderd van '3'.In CEN TC54 WG C SG-DC wordt dit op dezelfde manier aangepakt:
"Determine the three stress components (two direct and one shear) at each load condition with reference to some convenient fixed axes. For each stress component, calculate the maximum difference between the stresses. Calculate principel stresses from the resulting stress differences. delta_S is then the numerically greatest of these principel stresses."
Zowel NEN3650 alsmede D1200 dienden op dit punt te worden aangepast. Een en ander is destijds aan de TCTD gemeld. Dit heeft er mede toe geleid dat beide normen nu daadwerkelijk hierop zijn aangepast.
Genoemde methode is analytisch uit te voeren, dit in tegenstelling tot de vloei-ellips methode.
In ASME wordt als maximum toelaatbare waarde 3Sm genoemd. Verder wordt verwezen naar par 4-134. Volgens deze paragraaf is:
Hieruit volgt dat 3Sm overeen komt met Re + Re(vm). Dit is in overeenstemming met het gestelde in Stoomwezen blad D1200.
Stoomwezen blad D1101 (bovengrondse leidingen) neemt hier 0.8*[Re + Re(vm) voor i.v.m. relaxatie.